979. Distribute Coins in Binary Tree¶

Description¶

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

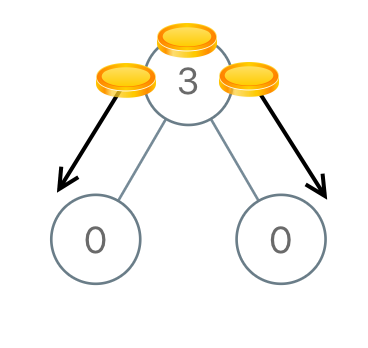
Example 1

Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

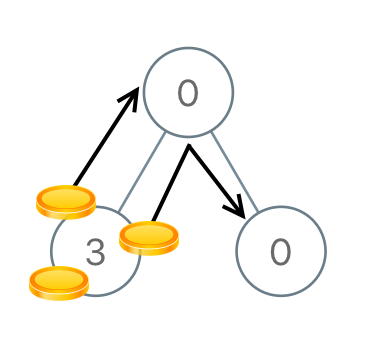
Example 2

Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Constraints

The number of nodes in the tree is n.
1 <= n <= 100.
0 <= Node.val <= n.
The sum of Node.val is n.

Solution: Depth-First Search¹¶

Time Complexity: O(n)
- We're visiting every node once. Therefore, the time complexity is O(n).
Space Complexity: O(n)
- In a balanced binary tree, the height is logarithmic in the number of nodes, which is O(log n). However, in the worst case, the height of the tree can be O(n) due to non-balanced binary tree like linked list or skewed tree. Therefore, the space complexity should be O(n).

We're using post-order traversal to calculate the number of moves required to make every node have exactly one coin. We're returning the absolute value of the number of coins in the left subtree and the right subtree.

Let say we have a tree like this:

graph TD;
    A(0) --> B(0);
    A --> C(2);
    B --> D(4);
    B --> E(0);
    C --> F(1);
    C --> G(0);

Here's how the distribution works:

The leftmost leaf node with 4 coins sends 3 coins to its parent. (3 moves)
The parent, now with 3 coins, sends 2 coins to its parent. (2 moves)
The right child of the root, with 2 coins, sends 1 coin to its parent. (1 move)

So, the total number of moves is 3 (from the leftmost leaf) + 2 (from its parent) + 1 (from the right child of the root) = 6 moves.

Typescript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function distributeCoins(root: TreeNode | null): number {
    function dfs(node: TreeNode | null): number {
        if (node == null) {
            return 0;
        }

        const leftCoins = dfs(node.left)
        const rightCoins = dfs(node.right)


        moves += Math.abs(leftCoins) + Math.abs(rightCoins)
        // If positive, the node has excess coins
        // If negative, the node needs coins
        return node.val = (node.val - 1) + leftCoins + rightCoins
    }

    let moves = 0
    dfs(root)
    return moves
};

Line 25-28 can be also written as:²

  const balance = leftCoins + rightCoins + node.val - 1
  moves += Math.abs(balance)
  return balance

Q: Why Does the Moves Need to Depend on the Number of Coins?¶

At first you might confuse why does the moves need to depends on the number of coins. This is because of the constraint of the problem that forces us to move exactly one coin at a time. So number of coins equals to the number of moves.

If you could move multiple coins at once, it would be much easier:

The leftmost leaf node with 4 coins sends 3 coins to its parent. (1 move)
The parent, now with 3 coins, sends 2 coins to its parent. (1 move)
The right child of the root, with 2 coins, sends 1 coin to its parent. (1 move)

So, the total number of moves is 3 if we could move multiple coins at once by using depth-first search.

979. Distribute Coins in Binary Tree¶

Description¶

Solution: Depth-First Search1¶

Q: Why Does the Moves Need to Depend on the Number of Coins?¶

Solution: Depth-First Search¹¶